[메모리 가상화 #3] 빈 공간 관리 본문
메모리 관리 시스템
모든 메모리 관리 시스템의 근본적인 측면, 구체적으로 빈 공간 관리에 관련된 문제를 논의 할 것이다.
- 고정 크기 공간 관리
- 메모리가 일정 크기로 나누어져있으면 리스트만 유지하다가 요청 시 첫번 째 블록을 반환하면 되어 간단
- 가변 크기 공간 관리
- malloc/free나 세그멘테이션처럼 크기가 다양한 빈 공간들로 구성되면 외부 단편화가 발생
- 총 빈 공간이 20바이트여도 10바이트짜리 두 개로 나뉘어 있으면, 15바이트 요청은 실패
핵심 질문
- 빈 공간을 어떻게 추적, 관리 할 것인가
- 가변 크기 요구를 만족시키면서 단편화를 최소화 하려면 어떤 전략을 써야할 까?
- 각 전략은 시공간 오버헤드가 어떻게 되는가?
가정
- 주로 사용자 수준 메모리 할당 라이브러리(예: malloc/free)의 역사와 기법에 초점을 맞춤
- void *malloc(size_t size)는 요청한 바이트 수를 나타내는 변수 size를 인자로 전달받고 요청된 크기와 같거나 큰 영역을 가리키는, 타입이 없는 또는 C 언어의 용어로 void 포인터를 반환
- void free(void *ptr)는 포인터를 인자로 전달받고 해당 영역을 해제
- free 호출 시 크기 정보를 전달하지 않으므로, 라이브러리는 내부 헤더에 저장된 메타데이터(size, 매직 넘버 등)로 블록 크기를 알아냅니다.
- 이 라이브러리가 관리 하는 공간은 역사적으로 힙(heap)이라 불리며, 힙의 빈 공간은 LinkedList나 이와 동등한 자료구조로 추적·관리
- 내부 단편화(요청보다 큰 블록을 반환하여 생기는 낭비)도 있지만, 외부 단편화(작은 조각으로 쪼개져 연속 공간이 부족해지는 현상)에 특히 중점
- 클라이언트에게 할당된 메모리는 다른 위치로 재배치될 수 다고 가정한다.
- malloc() 을 호출하여 받은 힙 일부 영역은 free()를 통하여 반환할 때까지 프로그램이 소유하게 되고, 라이브러리에 의해 다른 위치로 옮겨질 수 없다.
- 단편화 해결에 유용하게 사용되는 빈 공간의 압축은 이 경우에는 사용이 불가능하다.
저수준 기법 (분할과 병합)


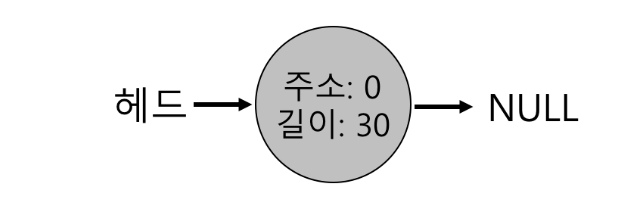
- 30바이트의 힙이 있다고 가정하자.
- 이 힙의 빈 공간 리스트에는 2개의 원소가 있다.
- 주소: 0 길이: 10
- 주소: 20 길이: 10
- 이 힙의 빈 공간 리스트에는 2개의 원소가 있다.
- 여기에 10바이트를 초과하는 모든 요청은 실패하여 NULL 반환
- 요청한 크기에 해당하는 메모리 청크가 없기 때문
- 만약 1바이트 메모리를 요청하면 ?
- 요청을 만족시킬 수 있는 빈 청크를 찾아 이를 둘로 분할한다.

- 만족시킬 수 있는 빈 청크를 찾아 이를 둘로 분할한다.
- 하나는 호출자에게 반환
- 남은 청크는 리스트에 남게된다.

- 이전 상황에서 만약 free(10)을 호출하여 힙의 중간에 존재하는 공간을 반환할 때, 이 빈공간을 다시 리스트에 추가하면 위와 같은 모양이 됨.
- 하지만 이러면 10바이트의 길이가 3개로 나누어져있음, 사용자가 20바이트를 요청하는 경우 단순한 리스트 탐색은 그와 같은 빈 청크를 발견하지 못하고 실패를 반환한다.
- 이를 방지하기 위해, 메모리 청크가 반환될 때 빈 공간들을 병합한다.
- 메모리 청크를 반환할 때 해제되는 청크의 주소와 바로 인접한 빈 청크의 주소를 살핀다.
- 새로 해제된 빈 공간이 왼쪽의 빈 청크와 바로 인접해 있다면(이 예에서는 양쪽으로) 하나의 더 큰 빈 청크로 병합한다.
- 병합 이후의 최종 리스트는 다음과 같은 모양이다.
할당된 공간 크기 파악
- free(void *ptr) 는 매개변수로 크기를 받지 않는다. 왜냐하면 추가 정보를 헤더블럭에 저장한다.
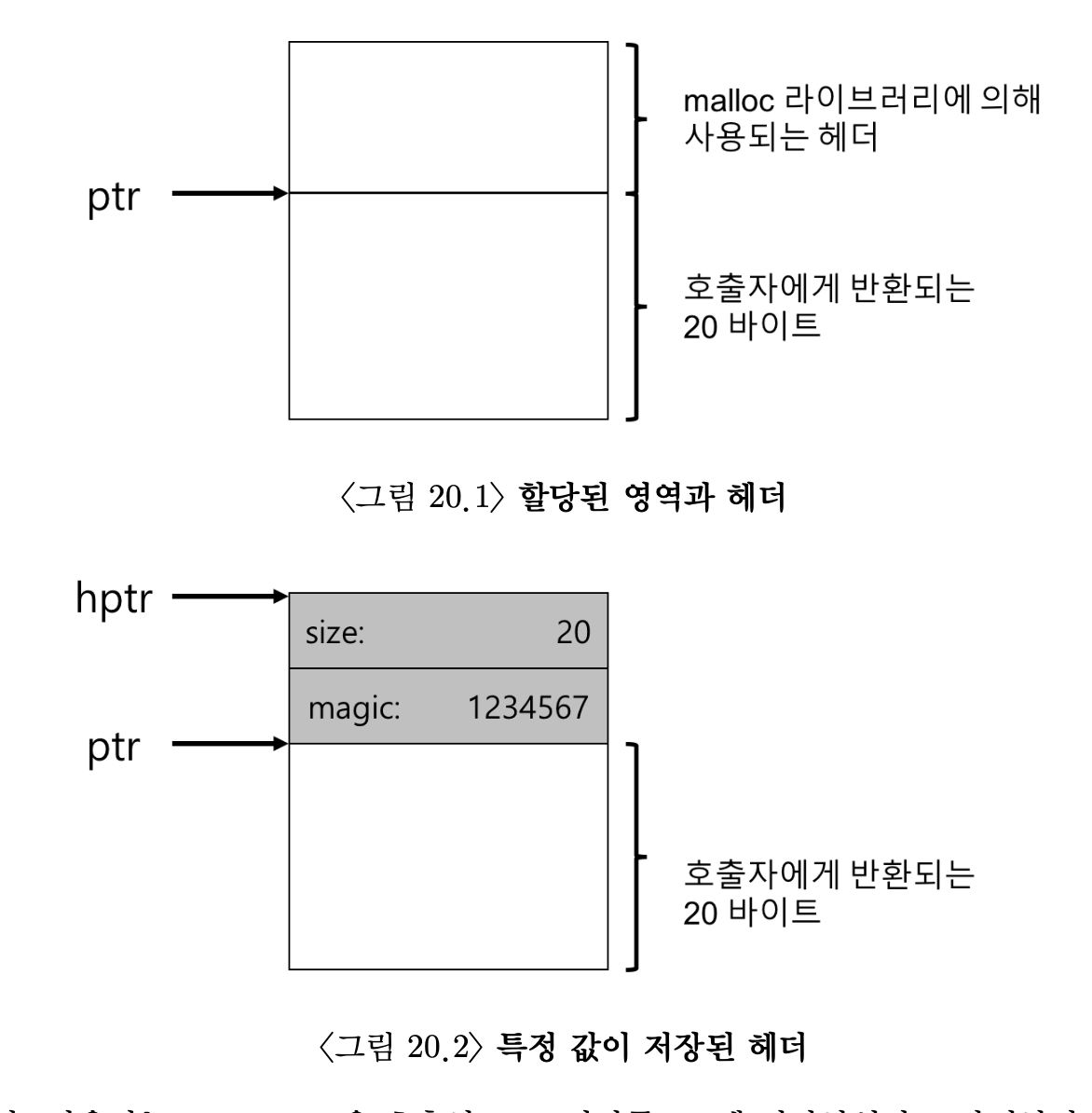
- 사용자는 malloc()을 호출하고 그 결과를 ptr에 저장하였다고 가정하자. 예를 들어, ptr = malloc (20);
- 헤더는 적어도 할당된 공간의 크기는 저장해야 한다(이 경우 20). 또한, 해제 속도를 향상시키기 위한 추가의 포인터, 부가적인 무결성 검사를 제공하기 위한 매직 넘버, 및 기타 정보를 저장할 수 있다.
- 다음과 같이 할당 영역의 크기와 매직 넘버를 저장하는 간단한 헤더를 가정하자.
// 그림 20.2 와 비슷
typedef struct __header_t {
int size;
int magic;
} header_t;
- 사용자가 free(ptr)을 호출하면 라이브러리는 헤더의 시작 위치를 파악하기 위해 간단한 포인터 연산을 한다.
void free(void *ptr) {
header_t *hptr = (void *)ptr - sizeof(header_t);
...
}
- 헤더를 가리키는 포인터를 알아내면 라이브러리는 매직 넘버가 기대하는 값과 일치하는지 비교하여 안정성 검사(sanity check)를 실시한다.
assert(htpr→magic == 1234567)
- 그리고 새로 해제된 영역의 크기를 계산한다. (헤더의 크기를 영역의 크기에 더함)
- 빈 영역의 크기는 헤더 크기 + 사용자에게 할당된 영역의 크기가 된다.
- 사용자가 바이트의 메모리 청크를 요청하면 라이브러리는 size만큼의 빈 청크를 찾는 것이 아니라 size + 헤더의 크기인 청크를 탐색한다.
빈 공간 리스트 내장
이제 이런 리스트를 빈 공간에 어떻게 구현할 수 있는가 ?
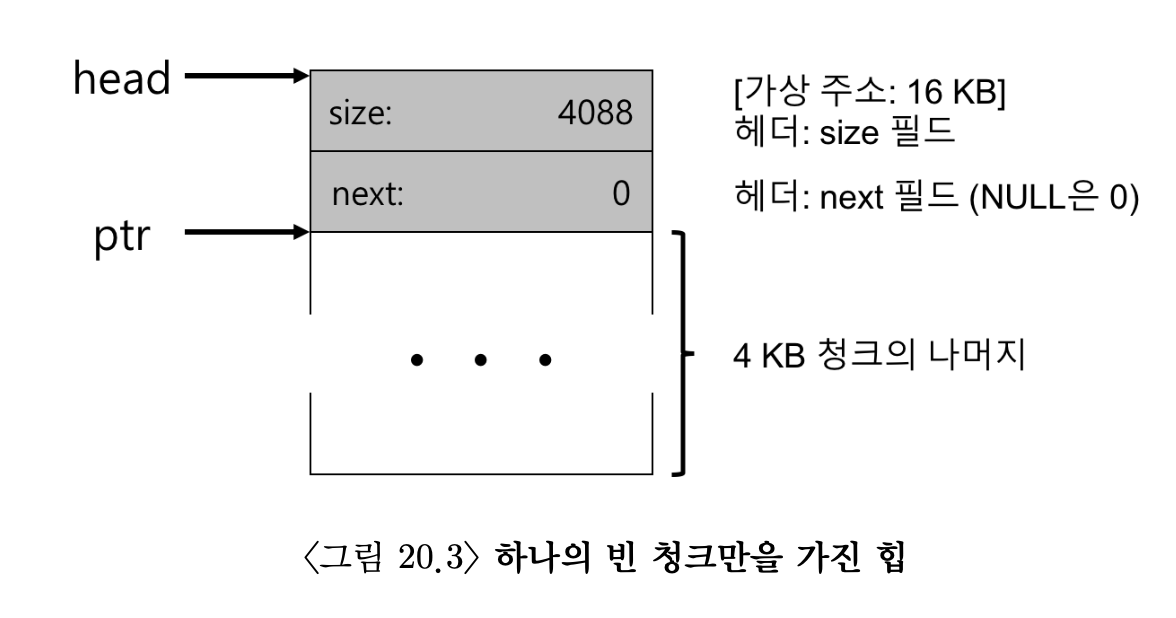
- 4KB의 힙이 있다고 가정해보자
- 이를 빈 공간 리스트로 관리하기 위해서 먼저 리스트를 초기화해야한다.
- 초기 리스트는 4096 - 헤더 크기 길이의 항목을 하나 가지고있다.
- 링크드리스트로 구현됨
typedef struct __node_t {
int size;
struct __node_t *next;
} node_t;
- 힙은 시스템 콜 mmap() 을 호출하여 얻어진 영역에 구축된다고 가정한다.
- 이 방법이 힙을구축하기 위한 유일한 방법은 아님
node_t *head = mmap(NULL, 4096, PROT_READ|PROT_WRITE, MAP_ANON[MAP_PRIVATE, -1, 0);
head->size = 4096 - sizeof(node_t);
head->next = NULL
- 이 코드의 실행 후 리스트는 크기 4088의 항목 하나만을 가지게 된다.
- head 포인터는 이 영역의 시작 주소를 담고 있다.
- 영역의 시작 주소를 16 KB라고 가정하자 이때 힙의 모양은 그림 20.3에서 보는 것과 비슷할 것이다.
- 이제 100바이트 메모리 청크가 요청되었다고 가정해보자
- 라이브러리는 충분한 크기의 청크를 찾는다. (하나의 빈 청크 4088) 만이 존재하기 때문에 이 청크가 선택된다.
- 요청을 처리하기에 충분한 크기, 앞서 말한것 처럼 빈 영역의 크기 + 헤더의 크기를 충족시킬 수 있는 청크와 나머지 빈 청크 두 개로 분할한다. (헤더의 크기를 8바이트라고 가정하면) 이제 힙의 공간 모습은 그림 20.4와 비슷하다.

- 100바이트에 대한 요청이 오면 라이브러리는 기존 하나의 빈 청크 중 108바이트를 할 당하고 할당 영역을 가리키는 포인터(그림의 ptr)를 반환한다.
- 그리고 나중에 free()에서 사용할 수 있도록 할당된 공간 직전 8바이트에 헤더 정보를 넣는다.
- 그런 후 남은 빈 노드를 3980바이트(4088-108)로 축소한다.
- 한번 더 100바이트씩 할당 하면 ? 그럼 20.5와 같다.

- 그림에서 볼 수 있듯이 힙의 시작 부분 324바이트가 현재 할당되어 있다. 3개의 헤더와 호출 프로그램에 의해 사용 중인 3개의 100바이트 영역을 볼 수 있다.
- 빈 공간 리스트는 여전히 head가 가리키는 하나의 노드로 구성되어 있지만 세 번의 분할 이후 3764바이트로 축소된 모습이다.
- 프로그램이 free()를 통해 일부 메모리를 반환하면 어떤 일이 벌어질까?
- 이 예제에서 응용 프로그램은 free(16500)을 호출하여 할당 영역 중 가운데 청크를 반환한다. 16500은 메모리 영역의 시작 주소 16384(1024*16 = 16KB), 이전 메모리 청크의 크기 108, 해제되는 청크의 헤더 8바이트를 모두 더해서 나온 값이다. 그림에서 이 값은 sptr이 나타낸다.
- 라이브러리는 신속히 빈 공간의 크기를 파악하고, 빈 청크를 빈 공간 리스트에 삽입한다. 빈 공간 리스트의 헤드 쪽에 삽입한다고 가정하면 공간의 모양은 그림 20.6과 같다.
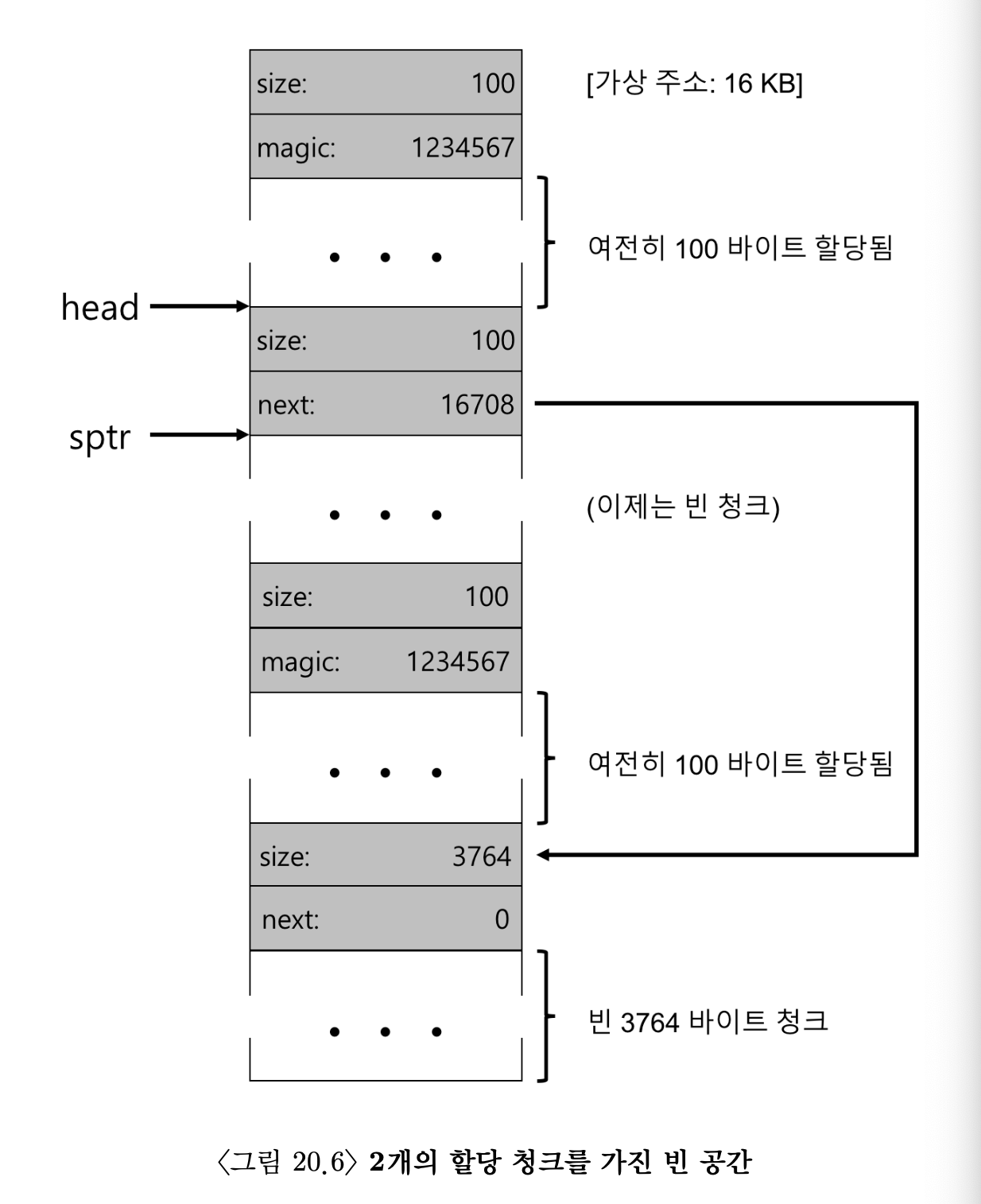
- 이제 빈 공간 리스트의 첫 번째 원소는 작은 빈 청크(100바이트 크기이며 리스트의 헤드가 가리킴)이고 두 번째 원소는 큰 빈 청크(3764바이트)이다.
- 불행하지만 흔히 일어나는 단편화가 생겼다.
- 마지막으로 마지막 2발의 사용 중인 청크가 해제된다고 하자. 병합이 없다면, 작은 단편으로 이루어진 빈 공간 리스트가 될 것이다(그림 20.7 참조).
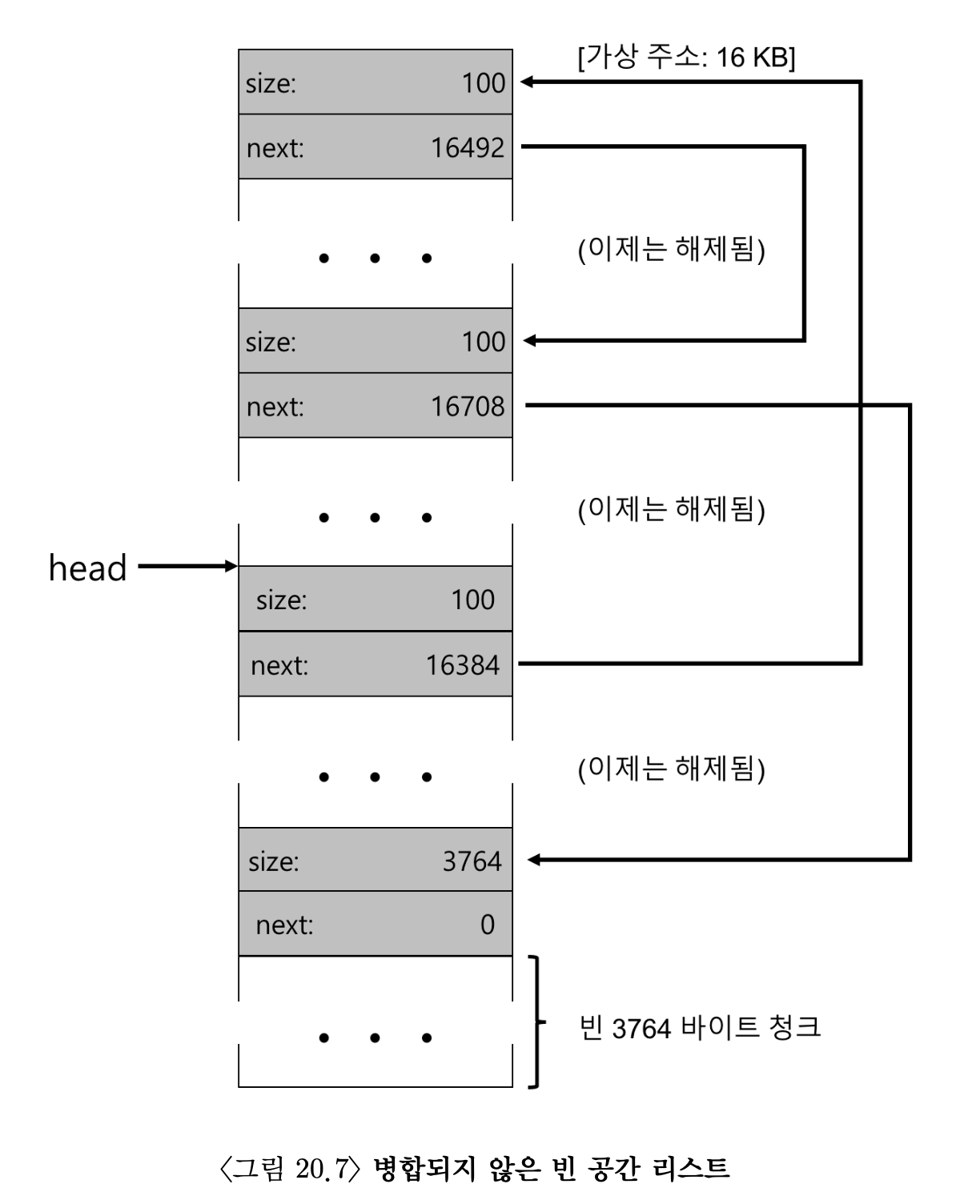
- 그림에서 볼 수 있듯이, 우리는 지금 큰 난관에 봉착했다.
- 모든 메모리가 비어 있긴 하지만, 전부 조각나 있기 때문에 한 청크가 아니라 단편으로 이루어진 메모리처럼 보인다.
- 해결책은 리스트를 순회하면서 인접한 청크를 병합하면 된다.
- 병합이 완료되면 힙은 전체 하나의 큰 청크가 된다.
힙의 확장
힙 공간이 부족한 경우에 어떻게 할 것인가?
- 가장 쉬운 방법은 단순히 실패(NULL)를 반환하는 것이다. 어떤 경우에는 이 방법이 유일한 대안일 수 있다.
- 대부분의 전통적인 할당기는 적은 크기의 힙으로 시작하여 모두 소진하면 운영체제로부터 더 많은 메모리를 요청한다.
- 할당기는 힙을 확장하기 위하여 특정 시스템 콜(예, 대부분의 Unix 시스템에서는 sbrk)을 호출한다.
- 그런 후 확장된 영역에서 새로운 청크를 할당한다.
- sbrk 요청을 수행하기 위해 운영체제는 빈 물리 페이지를 찾아 요청 프로세스의 주소 공간에 매핑한 후, 새로운 힙의 마지막 주소를 반환한다.
- 이제부터 더 큰 힙을 사용할 수 있고 요청은 성공적으로 충족될 수 있다.
기본 전략
빈 공간 할당을 위한 기본 전략에 대해 살펴보자
- 이상적인 할당기는 속도가 빠르고 단편화를 최소로 해야 한다.
- 불행하게도 할당과 해제 요청 스트림은 무작위, 결국 프로그래머에 의해 결정되기 때문에, 어느 특정 전략도 잘 맞지 않는 입력을 만나면 성능이 매우 좋지 않을 수 있다.
- 우리는 최선의 정책을 설명하는 것이 아니라 몇 가지 기본 정책에 대해 이야기하고 각각의 장점과 단점을 논의한다.
최적 적합(Best Fit)
- 정의
- 요청 크기 이상인 빈 청크들 중 가장 작은(가장 “딱 맞는”) 블록을 선택하여 할당한다.
- 동작
- 빈 공간 리스트 전체를 스캔하여 요청 크기 ≥ 청크 크기인 모든 후보를 모은다.
- 그중에서 크기가 가장 작은 청크를 반환한다.
- 장점
- 할당 후 남는 조각(fragment)이 작아져 내부 단편화를 줄이는 경향이 있다.
- 단점
- 항상 리스트 전체를 검색해야 하므로 탐색 비용이 높으며, 실행 속도가 느릴 수 있다.
- 작은 빈 조각들이 많이 남아 외부 단편화가 오히려 심화될 수도 있다.
최악 적합(Worst Fit)
- 정의
- 요청 크기 이상인 빈 청크들 중 가장 큰 블록을 선택하여 요청만큼만 할당하고, 나머지를 빈 리스트에 다시 남긴다.
- 동작
- 빈 공간 리스트 전체를 스캔하여 요청 크기 ≥ 청크 크기인 모든 후보를 모은다.
- 그중에서 크기가 가장 큰 청크를 반환하고, 잔여 부분을 새로운 빈 청크로 리스트에 유지한다.
- 장점
- 나머지 빈 공간이 큰 단일 블록으로 유지되므로, 이후 큰 요청을 처리할 가능성을 높다.
- 단점
- 전체 검색 비용이 높아 할당 속도가 느리다.
- 연구 결과, 예기치 못한 작은 조각이 많이 발생해 오버헤드가 커지는 경향이 있다.
최초 적합(First Fit)
- 정의
- 빈 공간 리스트를 앞에서부터 순차 탐색하여, 요청 크기 이상인 첫 번째 블록을 즉시 할당한다.
- 동작
- 리스트 헤드부터 순서대로 탐색
- 요청 크기 ≥ 청크 크기인 첫 블록을 발견하면 그 즉시 반환하고, 남은 부분은 리스트에 남김
- 장점
- 탐색을 후보가 발견되는 시점에 멈추므로 평균 탐색 비용이 낮아 빠르다.
- 단점
- 리스트 시작에 크기가 작은 객체가 누적될 수 있다.
- 주소 기반 정렬(address-based ordering) 등을 병행하지 않으면 병합이 어려워 외부 단편화가 누적될 수 있다.
다음 적합(Next Fit)
- 정의
- 리스트의 처음부터 탐색하는 대신 마지막으로 찾았던 원소를 가리키는 추가의 포인터를 유지한다.
- 동작
- 이전 할당이 일어난 위치를 가리키는 포인터를 유지
- 그 위치부터 리스트를 순회하면서 요청 크기 이상인 첫 블록을 할당
- 리스트 끝까지 못 찾으면 리스트 머리로 돌아가 다시 탐색
- 장점
- 리스트 앞쪽에 단편이 몰리는 현상을 줄여주어, 최초 적합과 유사한 속도에 단편 집중 완화 효과를 기대할 수 있다.
- 단점
- 여전히 전체 구간을 순회해야 할 수 있어, 극단적인 워크로드에서는 탐색 비용이 높아질 수 있다.
출처 : 운영체제 아주 쉬운 세가지 이야기
'Fundamentals > OS' 카테고리의 다른 글
| [메모리 가상화 #5] 페이징: TLB (1) | 2025.07.01 |
|---|---|
| [메모리 가상화 #4] 페이징 (1) | 2025.06.30 |
| [메모리 가상화 #2] 세그멘테이션 (0) | 2025.06.28 |
| [메모리 가상화 #1] 멀티프로그래밍, 주소공간, 주소공간 변환 (2) | 2025.06.20 |
| [CPU 스케줄링 #3] 멀티 프로세서 SQMS, MQMS (1) | 2025.06.17 |
Comments



